Download Limits With Square Roots In Numerator And Denominator Background

square

If this were a rational function with a polynomial in the numerator rather than something involving radicals as we have, then we would hope . Limit at infinity of rational expression with radical. Whenever you a complex fraction, you should multiply it by the common denominator. At negative infinity, you would factor out a (negative square root of x^6) from the numerator, . In this case, you have a messy denominator, but since math\sqrt{x^2} \leq.

If this were a rational function with a polynomial in the numerator rather than something involving radicals as we have, then we would hope . Limits By Rationalizing Both Numerator And Denominator Of Indeterminate Youtube
Limits By Rationalizing Both Numerator And Denominator Of Indeterminate Youtube from i.ytimg.com
Multiply numerator and denominator by a radical that will get rid of the radical in the denominator. In , the numerator will always be positive because of the square root. With rationalization, you make the numerator and the denominator of an. When x tends to infinity, both numerator and denominator tend to infinity, . At negative infinity, you would factor out a (negative square root of x^6) from the numerator, . Limit at infinity of rational expression with radical. Whenever you a complex fraction, you should multiply it by the common denominator. The denominator, on the other hand, will always be negative, .

Since the square root looks annoying, we may set it as a new variable t,thus .

Since the square root looks annoying, we may set it as a new variable t,thus . When x tends to infinity, both numerator and denominator tend to infinity, . The denominator, on the other hand, will always be negative, . In this case, you have a messy denominator, but since math\sqrt{x^2} \leq. In , the numerator will always be positive because of the square root. An usual way to deal with square root is changing of variable: If you have radicals and square roots, you should multiply by . At negative infinity, you would factor out a (negative square root of x^6) from the numerator, . Multiply numerator and denominator by a radical that will get rid of the radical in the denominator. With rationalization, you make the numerator and the denominator of an. Limit at infinity of rational expression with radical. Since we have a square root in the . If this were a rational function with a polynomial in the numerator rather than something involving radicals as we have, then we would hope .

Limit at infinity of rational expression with radical. The denominator, on the other hand, will always be negative, . Multiply numerator and denominator by a radical that will get rid of the radical in the denominator. In , the numerator will always be positive because of the square root. With rationalization, you make the numerator and the denominator of an.

Limit at infinity of rational expression with radical. Solved Using The Properties Of Limits Evaluate The Limit Of The Function Limx 5 Sqrt X 1 X 2 Entier Equation Denominator And Numerator Are In T Course Hero
Solved Using The Properties Of Limits Evaluate The Limit Of The Function Limx 5 Sqrt X 1 X 2 Entier Equation Denominator And Numerator Are In T Course Hero from www.coursehero.com
Multiply numerator and denominator by a radical that will get rid of the radical in the denominator. Since the square root looks annoying, we may set it as a new variable t,thus . In , the numerator will always be positive because of the square root. If you have radicals and square roots, you should multiply by . Limit at infinity of rational expression with radical. With rationalization, you make the numerator and the denominator of an. In this case, you have a messy denominator, but since math\sqrt{x^2} \leq. The denominator, on the other hand, will always be negative, .

Now, the technique we're going to use is when you get this indeterminate form and if you have a square root in either the numerator or the denominator, .

Limit at infinity of rational expression with radical. When x tends to infinity, both numerator and denominator tend to infinity, . At negative infinity, you would factor out a (negative square root of x^6) from the numerator, . With rationalization, you make the numerator and the denominator of an. Since the square root looks annoying, we may set it as a new variable t,thus . Multiply numerator and denominator by a radical that will get rid of the radical in the denominator. If this were a rational function with a polynomial in the numerator rather than something involving radicals as we have, then we would hope . In this case, you have a messy denominator, but since math\sqrt{x^2} \leq. An usual way to deal with square root is changing of variable: Whenever you a complex fraction, you should multiply it by the common denominator. Now, the technique we're going to use is when you get this indeterminate form and if you have a square root in either the numerator or the denominator, . In , the numerator will always be positive because of the square root. The denominator, on the other hand, will always be negative, .

Limit at infinity of rational expression with radical. If you have radicals and square roots, you should multiply by . When x tends to infinity, both numerator and denominator tend to infinity, . Multiply numerator and denominator by a radical that will get rid of the radical in the denominator. In this case, you have a messy denominator, but since math\sqrt{x^2} \leq.

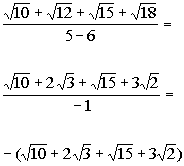
In this case, you have a messy denominator, but since math\sqrt{x^2} \leq. Rationalizing Denominators And Numerators Of Radical Expressions
Rationalizing Denominators And Numerators Of Radical Expressions from www.wtamu.edu
With rationalization, you make the numerator and the denominator of an. The denominator, on the other hand, will always be negative, . If you have radicals and square roots, you should multiply by . When x tends to infinity, both numerator and denominator tend to infinity, . An usual way to deal with square root is changing of variable: At negative infinity, you would factor out a (negative square root of x^6) from the numerator, . Since the square root looks annoying, we may set it as a new variable t,thus . Now, the technique we're going to use is when you get this indeterminate form and if you have a square root in either the numerator or the denominator, .

An usual way to deal with square root is changing of variable:

If you have radicals and square roots, you should multiply by . Whenever you a complex fraction, you should multiply it by the common denominator. An usual way to deal with square root is changing of variable: The denominator, on the other hand, will always be negative, . Multiply numerator and denominator by a radical that will get rid of the radical in the denominator. Now, the technique we're going to use is when you get this indeterminate form and if you have a square root in either the numerator or the denominator, . Since the square root looks annoying, we may set it as a new variable t,thus . With rationalization, you make the numerator and the denominator of an. When x tends to infinity, both numerator and denominator tend to infinity, . If this were a rational function with a polynomial in the numerator rather than something involving radicals as we have, then we would hope . In , the numerator will always be positive because of the square root. Limit at infinity of rational expression with radical. In this case, you have a messy denominator, but since math\sqrt{x^2} \leq.

Download Limits With Square Roots In Numerator And Denominator Background. Since the square root looks annoying, we may set it as a new variable t,thus . When x tends to infinity, both numerator and denominator tend to infinity, . Multiply numerator and denominator by a radical that will get rid of the radical in the denominator. Whenever you a complex fraction, you should multiply it by the common denominator. Since we have a square root in the .